Explanation
To determine the number of additional 5-star ratings you need to achieve a desired average rating, we use simple algebra.
Here’s a step-by-step explanation:
1. Define the Variables:
- Let the Current Average be the current average rating.
- Let the Current Count be the current number of ratings.
- Let the Desired Average be the desired average rating.
- Let x be the number of additional 5-star ratings needed
2. Set up the Equation
- The total sum of the ratings currently is Current Average× Current Count
- The total sum of the ratings after adding x more 5-star will be: ( Current Average × Current Count )+(5 X x)
- The total number of ratings after adding x more ratings will be Current Count + x
3. Create the Equation:
Now to get the Desired Average, we use the following equation:
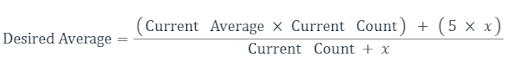
4. Solve for x :
- Multiply both sides by Current Average + x to clear the denominator:
Desired Average × (Current Average+x)=(Current Average × Current Count)+(5 X x)
- Expand and rearrange to solve for x : ( Desired Average × Current Count + Desired Average × x = Current Average × Current Count + 5x)
- Combine like terms: ( Desired Average × Current Count − Current Average × Current Count= 5x − Desired Average × x )
- Then: Desired Average−Current Average×Current Count = x 5 − Desired Average

And that is how we get the number of ratings needed to achieve a desired rating.
Example:
Let’s suppose we have a product with the following details:
- Current Average = 3.93
- Current Count = 57
- Desired Average = 4.5
Plugging those values into the equation:
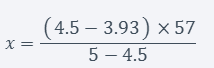
Let’s calculate it:
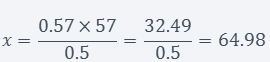
And since you can’t have a fraction of a rating, you would need at least 65 additional 5-star ratings to reach an average of 4.5.




